Série 8

Objectifs

Comprendre les concepts liés à la boucle while et les mettre en œuvre.

Identifier les différentes étapes importantes dans la conception d'une boucle.

Décomposer et créer une procédure qui s'occupe de traiter une itération.

Notions pour la série

Démarche de résolution de problèmes

Squelette du programme

Contraintes impératives

Les différents programmes que vous devez réaliser seront nommés ALP-S8Ex1 à ALP-S8Ex3 et se trouveront dans un dossier nommé ALP-S8.

Énoncé

Exercice T1

Réaliser un programme qui affiche une spirale rectangle, en partant de l'intérieur vers l'extérieur. La spirale est basée sur une longueur de côté initial, un incrément et une longueur maximale. Le dessin s'arrête dès que la longueur d'un côté dépasse le maximum admis.

Vous n'avez pas besoin de valider les données pour cet exercice.

Exemples

Longueur initiale 10, incrément 4, longueur maximale 10:

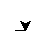
Longueur initiale 10, incrément 4, longueur maximale 9:

Aucun dessin

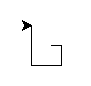
Longueur initiale 10, incrément 4, longueur maximale 14:

Longueur initiale 10, incrément 10, longueur maximale 41:

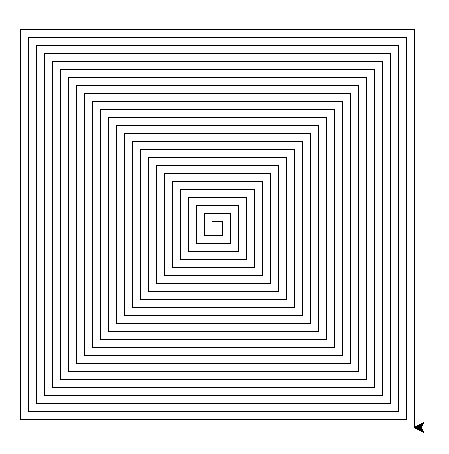
Longueur initiale 10, incrément 4, longueur maximale 400:

Astuce: l'instruction speed(-1) accélère grandement le dessin!

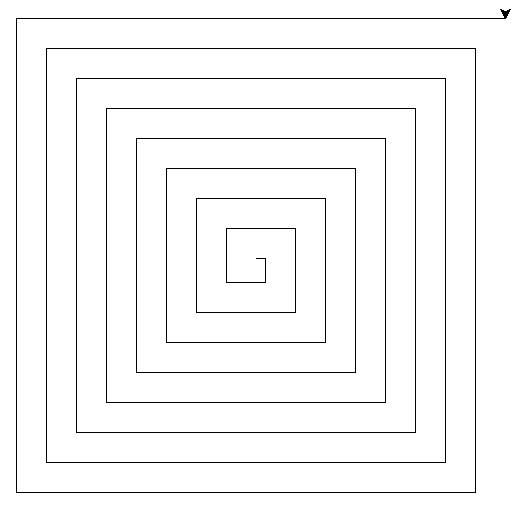
Longueur initiale 9, incrément 10, longueur maximale 330:

Astuce: l'instruction speed(-1) accélère grandement le dessin!

Ajouter une fonctionnalité

Votre programme doit afficher la spirale en alternant les couleurs de chaque côté dans l'ordre suivant 'yellow', 'green', 'blue', 'red'.

Longueur initiale 10, incrément 4, longueur maximale 400:

Astuce: l'instruction speed(-1) accélère grandement le dessin!

Exercice T2

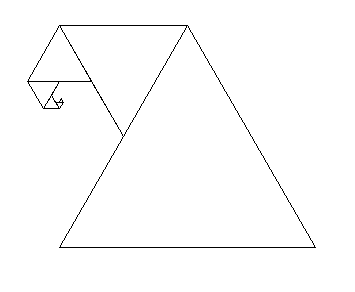
Développez un programme qui dessine la figure de l’illustration ci-dessous. Commencez par dessiner le plus grand triangle dont la longueur des côtés est saisie par l'utilisateur. La mesure du côté suivant est deux fois plus courte. Votre programme doit dessiner des triangles jusqu’à ce que le côté du triangle à dessiner devienne plus petit que 3.

Veillez à bien décomposer votre programme en fonctions et procédures. La validation des données n'est pas requise.

Astuce: Utilisez speed(-1) et hideturtle()

Avec une longueur de côté initiale de 10:

Avec une longueur de côté initiale de 256:

Exercice 1

Afficher les premiers termes de la suite de Fibonacci jusqu'à l'ordre n. La donnée n doit être positive ou nulle.

La suite de Fibonacci est définie par :

F0=0
F1=1
Fk=Fk-2 + Fk-1       pour k > 1

Exemple de résultat (pour n = 9) :

F(0) = 0
F(1) = 1
F(2) = 1
F(3) = 2
F(4) = 3
F(5) = 5 
F(6) = 8
F(7) = 13
F(8) = 21
F(9) = 34   

Que pouvez-vous observer ?

Contrainte impérative : La donnée n sera validée au moyen d'une fonction à résultat booléen.

Exercice 2

Idem exercice 1 (Fibonacci), mais demander à l'utilisateur non pas n, mais la valeur de fin.

Exemple de résultat (pour fin = 15) :

F(0) = 0
F(1) = 1
F(2) = 1
F(3) = 2
F(4) = 3
F(5) = 5    
F(6) = 8
F(7) = 13

Exercice 3

Écrivez une procédure qui permet d'afficher/dessiner les triangles ci-dessous. Les données seront le type de triangle (1, 2, 3 ou 4) ainsi que le nombre de lignes du triangle.

Remarque: pour afficher les triangles type 3 et 4, il faut afficher le bon nombre d'espaces avant les étoiles.

Contraintes impératives :

• Les données seront validées au moyen d'une fonction à résultat booléen.
• Vous prendrez bien soin d'identifier les différentes tâches et sous-tâches à accomplir que vous traduirez par des procédures dont vous définirez soigneusement les paramètres.

Aide : commencez par faire une procédure qui affiche un carré de nb lignes contenant chacune nb étoiles. Adaptez ensuite cette(ces) procédure(s) pour faire les différents triangles.