TP5 - Donées climatiques
Dans ce TP nous allons travailler avec des données scientifiques réelles. Il s'agit de données de mesure de la température de l'hémisphère nord entre les années 1850 et 2018.
Les données sont issues du site https://crudata.uea.ac.uk/cru/data/temperature. Il s'agit du jeu de données CRUTEM4-nh.dat (températures au-dessus de la terre pour l'hémisphère nord) en sa version du 28.10.2019.
Elles ont été simplifiées et se présentent comme suit:
| année | moyenne janvier | moyenne février | ... | moyenne décembre |
|---|
Il y a donc 169 lignes (années 1850 à 2018) et 13 colonnes (l'année puis une valeur pour chaque mois).
Voici comment ces données se présentent concrètement:
[[1850. -3.061 0.579 ... -1.285 -0.38 -0.269]
[1851. 0.288 -0.384 ... 0.37 -0.509 -0.323]
[1852. -0.274 -0.447 ... -0.563 -0.83 1.118]
...
[2016. 1.661 2.607 ... 0.973 0.91 1.281]
[2017. 1.619 1.969 ... 1.024 1.091 1.375]
[2018. 1.136 1.156 ... 1.135 0.728 1.057]]Comme il est coûtume dans la communauté scientifique, les températures sont exprimées sous-forme d'anomalie (différence) par rapport à la température moyenne des années 1961 à 1990. Cette valeur est estimée à 14°C, mais notez qu'il n'est pas valable d'additionner une anomalie à cette valeur pour obtenir la température absolue.
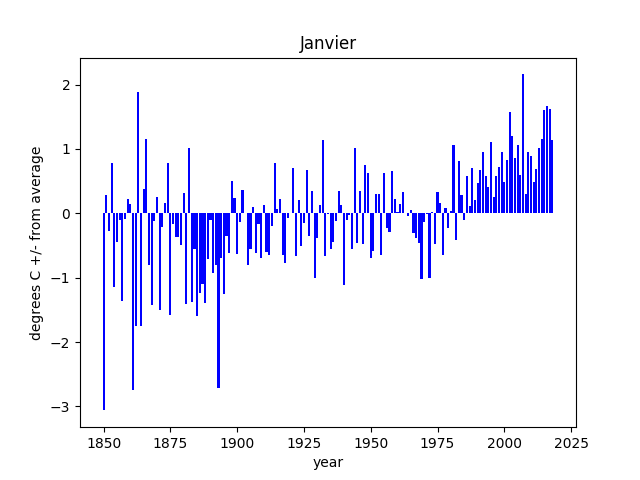
Voici un diagramme représentant les valeurs pour le mois de janvier:
Infos pratiques
Fichier à compléter
Fichier de données à utiliser
Nous allons utiliser les librairies numpy et matplotlib. Selon la configuration de votre installation de Thonny, ces librairies ne sont pas disponibles. Il faut dans ce cas les installer, comme expliqué dans cette vidéo.
Tâche 1 : Moyennes annuelles
Pour estimer l'évolution du climat, il peut être utile de considérer uniquement la moyenne annuelle des anomalies de température. Ecrivez une fonction qui calcule et retourne la moyenne annuelle pour chaque année dans un tableau numpy à une dimension.
Un tel tableau peut être initialisé comme suit: moyannuelle = np.zeros(nbelements).
Ensuite, affichez le résultat à l'aide de la fonction plotanomalies.
Les premières et dernières moyennes attendues sont:
[-0.6 -0.21441667 -0.35891667 ... 1.30041667 1.0735 0.97958333]
ATTENTION la dernière moyenne (2019) n'est pas tout à fait juste (mois à 0 car encore inconnues) - corriger pour 2020-21
Voici le graphique attendu:
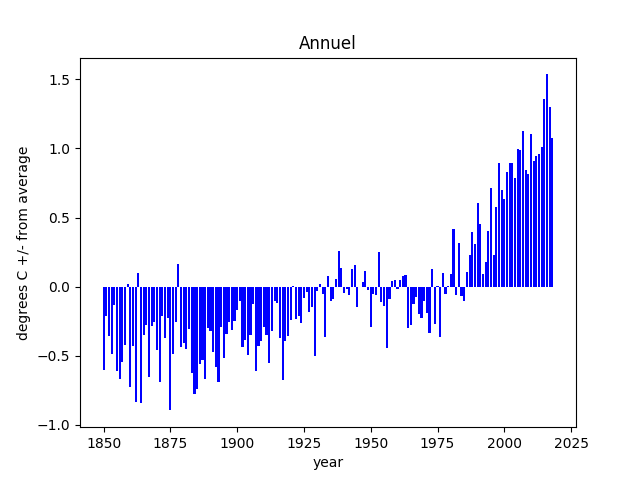
Nous constatons que les moyennes annuelles sont moins fluctuantes que les moyennes pour un seul mois (Janvier ci-dessus) et que c'est donc plus facile d'identifier des tendances.
Est-ce que la planète se réchauffe?
Tâche 2 : Moyennes des anomalies pour un intervalle d'années donné
Ici nous allons calculer, pour chaque mois, ainsi que pour les moyennes annuelles, la moyenne des anomalies entre les années 1961 et 1990 (inclusives).
Préparatif
Pour ce faire, nous allons tout d'abord ajouter les moyennes annuelles en tant que dernière colonne à notre tableau global. Vous pouvez utilisez l'une des solutions suivantes pour ce faire:
datacomplet = np.c_[data, moyannuelle]datacomplet = np.insert(data, data.shape[1], values=moyannuelle, axis=1)(Le deuxième paramètre est la position d'insertion)datacomplet = np.append(data, moyannuelle.reshape((moyannuelle.shape[0], 1)), 1)
Afficher le tableau datacomplet pour vérifier le succès de l'opération:
[1850. -3.061 0.579 ... -0.38
-0.269 -0.6 ]
[1851. 0.288 -0.384 ... -0.509
-0.323 -0.21441667]
[1852. -0.274 -0.447 ... -0.83
1.118 -0.35891667]
...
[2017. 1.619 1.969 ... 1.091
1.375 1.30041667]
[2018. 1.136 1.156 ... 0.728
1.057 1.0735 ]
[2019. 1.385 1.312 ... 0.
0. 0.97958333]]Conseils
Il s'agit ici de calculer une moyenne par colonne (pour chaque mois et pour les moyennes annuelles).
Une difficulté supplémentaire sera l'ajout de l'intervalle d'années à prendre en compte. Dans un premier temps, nous vous conseillons de faire la moyenne par colonne sans cet intervalle de filtrage.
Le résultat attendu pour cette première étape (moyenne par colonne sans filtre) est:
[-0.03992353 -0.09103529 -0.25574706 -0.09847059 -0.05588235 0.06258235
0.10188824 0.10862941 0.06390588 0.0153 -0.17199412 -0.15170588
-0.04270441]Vous allez maintenant faire en sorte que la moyenne soit calculée uniquement pour un intervalle d'années données. Vous pouvez commencer par mettre cet intervalle en dur (1961-1990), mais ensuite il serait bien de rendre cela paramétrable.
Le résultat attendu pour les années 1961 à 1990 est:
[0.00616667 0.0097 0.0035 0.0095 0.0051 0.00423333
0.00453333 0.00433333 0.0052 0.0081 0.0037 0.00606667
0.00584444]Le résultat pour les années 1991 à 2000 est:
[0.6695 0.9478 0.5034 0.5622 0.413 0.454
0.3929 0.4155 0.3157 0.4149 0.2675 0.4887
0.48709167]Le résultat attendu pour les années 2001 à 2018:
[1.09861111 1.10627778 1.23122222 1.08438889 0.93083333 0.93933333
0.89238889 0.92627778 0.92861111 1.02011111 1.099 0.98672222
1.02031481]Tâche 3 : Années extrêmes
Créer le code nécessaire pour trouver et afficher l'année la plus chaude (c'est dire dont la moyenne des anomalies est la plus élevée) et l'année la plus froide. Il faut afficher également l'anomalie correspondant à chacune de ces années.
Affichage attendu:
Année la plus froide: 1875 (-0.896)
Année la plus chaude: 2016 (1.536)Difficulté avancée (vraiment)
Faites la même chose pour les 3 années les plus chaudes et les 3 années les plus froides. Ensuite, rendez le nombre d'année paramétrable afin que l'utilisateur puisse l'indiquer (par exemple les 5 ou les 10 années les plus extrêmes).
Exemple de résultats (4 années les plus froides, puis 4 années les plus chaudes):
array([[1875. , -0.89566667],
[1864. , -0.83908333],
[1862. , -0.83241667],
[1884. , -0.77633333],
[2016. , 1.536 ],
[2015. , 1.36008333],
[2017. , 1.30041667],
[2007. , 1.1255 ]])Tâche 4 : Température moyenne par décennie
Créer le code nécessaire pour afficher la moyenne par décennie (1850-1859, 1860-1869, ... , 2000-2009, 2010-2018) et qui indique la décennie la plus chaude et la décennie la plus froide.
L'approche conseillée est de calculer d'abord un nouveau tableau contenant la température (anomalie) moyenne par décennie, mais ce n'est pas forcément nécessaire.
Des fonctions créées lors de la tâche 2 devraient pouvoir vous faciliter grandement cette tâche.
Résultats obtenus (en brut), à vous de mettre en forme de manière convenable.
(1850, 1859): -0.4028666666666667,
(1860, 1869): -0.45585833333333337,
(1870, 1879): -0.388025,
(1880, 1889): -0.5363916666666666,
(1890, 1899): -0.4040583333333333,
(1900, 1909): -0.35034166666666666,
(1910, 1919): -0.3534333333333333,
(1920, 1929): -0.18922500000000003,
(1930, 1939): -0.010741666666666658,
(1940, 1949): 0.013691666666666663,
(1950, 1959): -0.08619166666666667,
(1960, 1969): -0.10149166666666667,
(1970, 1979): -0.10725000000000003,
(1980, 1989): 0.163825,
(1990, 1999): 0.48456666666666665,
(2000, 2009): 0.8803916666666668,
(2010, 2018): 1.117425Les décennies les plus extrêmes sont:
Décennie la plus froide (1880-1889) avec une anomalie moyenne de -0.54 °C
Décennie la plus chaude (2010-2018) avec une anomalie moyenne de 1.12 °C